Breaking state channels with TLA+
June 12, 2020
So far in this series we’ve covered a number of important state channel topics. One of these was the fundamental guarantee of state channels: that assuming chain liveliness, and lack of censorship, a participant should be able to withdraw their funds in a finite amount of time. We introduced a toy model of the state channel exit game, and showed that it provided the guarantee.
In order to support real-world applications, we need to move beyond the toy model to a more advanced state channel system. Can we be sure that the fundamental guarantee still holds? In this post we explain how we used the TLA+ verification tool to test our protocol, and how we fixed the issues that it detected.
What is TLA+ and why are we using it?
Ever since the release of the force-move paper, our team had been searching for some way to prove the correctness of the protocol. State channels involve multiple parties interacting both on-chain and off-chain, so it can be difficult to think through all the possibilities. We were fairly convinced that the protocol was good, but every now and then we’d think of a new edge-case, and would get worried for a bit until we could convince ourselves that it was handled. We wanted to find a way to remove the possibility of finding an unhandled case in the future, and remove any niggling doubts over the soundness of the protocol.
What exactly are we trying to show here? Back in the post on channel funding we introduced the guarantee mentioned in the introduction: that assuming chain liveliness, and lack of censorship, a participant should be able to withdraw their funds in a finite amount of time. We want to show that our state channel system has this property. In particular we want to show that, armed with the states exchanged in the channel, Alice has a path to reaching a finalized outcome on-chain, within a finite amount of time, no matter what actions any other party takes. Moreover, the outcome should be ‘recent’, in that it should have a turn number at least as large as the current state of the channel for Alice.
We initially started investigating a formal verification of the smart contracts, but while important for other reasons, it soon became clear that this wouldn’t be enough to provide the guarantees that we were looking for. Formal verification of the smart contracts would give us confidence that we’d implemented the protocol correctly, but didn’t appear to be useful for proving that the protocol itself had the properties we wanted. For example, it could show that if you submitted a force-move with a correctly signed state, then a challenge would be registered, but couldn’t show that there was always a sequence of force-move operations that one participant could call in order to exit in a finite time, no matter what actions the other participants were to take.
It was against this background that Andrew came across TLA+, and realised it might be just what we need.
TLA+ is a formal specification language. It is used to build a model of an algorithm or system, and then programmatically check that this model has certain properties. It was released by Leslie Lamport in 1999, and was used to write formal proofs of correctness for Byzantine Paxos. More recently it has found uses in industry, including by the engineering team at AWS, who used it to find and fix concurrency problems in DynamoDB.
Due to the capabilities of TLA+, some people describe it as exhaustively testable pseudocode. It’s this aspect that makes it suitable for what we want to do. We realised we could build a model of our adjudicator, and the channel participants who can interact with it. Using this we could use TLA+ to search through all the possible sequences of allowed operations, to identify scenarios where Alice doesn’t manage to withdraw her funds within some specified time interval. What’s more, if we managed to prove a statement along the lines of “for all possible sequences of operations of length n, Alice manages to withdraw her funds within m < n steps” by exhaustive search, then we also know that Alice must always be able to withdraw her funds within m steps, and so will have proved the safety of the protocol.
Insights gained
This section summarises the application of TLA+ to three successive versions of the protocol, from the initial proposal to the current version. The code for the model, along with instructions to recreate the results yourself, can be found in this repo.
We’ve decided to present the insights before digging into the model itself, as we anticipate that they’ll be of greater interest to the majority of people. If you’re someone who likes to understand all the details, you might want to skip to the “Model” section at the end, and read that first.
Attempt 1
Our starting point is a gas-optimized version of the protocol defined in the force-move paper. The protocol is pretty similar to the toy model covered in Playing the State Channel Exit Game post, with the difference it is possible to ‘recover’ from a challenge and continue the interaction off-chain, instead of having to finalize after the first challenge is launched. In an attempt to prevent infinite loops of challenges, the adjudicator keeps track of the turn number of the latest supported state that it has witnessed, and only allows challenges that could increase this number. The methods for interacting with the adjudicator can be summarised as follows:
| State | Action | NextState | Requirements |
|---|---|---|---|
| Open(n) | forceMove(m,s*,p) | Chal(m,s,p) | m >= n |
| Chal(n,s,p) | respond(n+1,s’,s) | Open(n+1) | s->s’ |
| Chal(n,s,p) | refute(m,s’,s) | Open(n) | m > n, p signed s’ |
| Chal(n,s,p) | altRespond(n+1,s,s’*) | Open(n+1) |
There is one way of launching a challenge: the forceMove(m,s*,p) operation, which
requires a supported state s* with turn number m, and must be launched by a channel
participant p. Provided that m is higher than the on-chain turn number, the channel
transitions to the challenge state, Chal(m,s,p).
There are three ways of responding to a force-move, respond, refute, and altRespond:
respond: the ‘expected’ way to respond to the challenge- The responder provides the next state, after which the interaction can continue off-chain.
- On-chain turn counter increases, because response state extends the supported challenge state to create a later supported state
refute: a way to respond to a stale challenge- The responder provides a later state signed by the challenger.
- This demonstrates provable bad behaviour on behalf of the challenger, so there’s an opportunity to build slashing into the protocol here
- It’s also efficient, as we don’t need to check any state transitions
- The on-chain turn counter can’t increase, as the participants just see a state, which doesn’t necessarily give them a new supported state
altRespond: needed to support situations when a participant signs multiple states with the same turn number- The responder provides a new supported state that advances the turn number by 1. On-chain turn counter increases as a later supported state is seen.
- This is the responder saying “you challenged in state
s, but you’d previously sent mes', and I want to move on from there instead”
In all cases, due to the performance optimizations, it’s also necessary to provide a copy
of the challenge state s, as in the optimized version only the hash of s is stored
on-chain. As you’ll see, this seemingly minor change turned out to have considerable
implications for the soundness of the protocol.
The TLA+ Verdict
We coded up this model and ran it through TLA+. It didn’t like it at all 🙈, and identified the following failure scenario:
- Start in state
Open(n) - Alice calls
forceMove(n,s*, Alice) - Eve front-runs with
forceMove(n,s*, Eve), putting the adjudicator in stateChal(n, s, Eve). - Alice’s force-move from step 2 fails.
- Eve calls
refute(n+k,s,s')wherekis bigger than one, chosen so that it is Eve’s turn, ands'is any valid state with turn numbern+k. The channel returns to stateOpen(n). - Go to step 1.
TLA+ found an infinite loop that enables Eve to keep the funds locked in the channel indefinitely! Of course Eve does have to pay, but then again Alice is also losing funds on each of her failed transactions. The griefing ratio is pretty favourable for Eve: she only needs to submit two transactions to Alice’s one (plus the premium to ensure she successfully front-runs each time). In any case, there’s a massive hole in the protocol. (We were actually semi-aware of this problem beforehand, but we were not aware of an attack as succinct as the one found by TLA+.)
The fix here isn’t obvious. The loop is due to the fact that refute doesn’t increase the
on-chain turn counter, because the participants don’t necessarily see a new supported
state. The only way to ensure there’s a new supported state is through validating a
transition on-chain, but the whole point of refute was to be able to cancel a provably
bad challenge, without having to spend gas to run the transition function on-chain.
One approach we considered was to store a list of the participants who had successfully called a force-move at the current turn counter on the chain, to enforce that no participant could call force-move more than once for each value of the turn counter. We decided this would be too complex and/or gas inefficient, given that there’s no constraint on the number of participants in a channel.
In the end we decided to simplify the protocol by removing the refute action altogether.
It didn’t seem too bad to lose the optimized way of responding to a stale challenge, as we
still have the option of introducing slashing in this case, along with a refund of gas
costs for the responder, which seems like a better way of incentivizing the correct
behaviour.
Attempt 2
After removing refute, we were left with the following set of operations:
| State | Action | NextState | Requirements |
|---|---|---|---|
| Open(n) | forceMove(m,s*,p) | Chal(m,s,p) | m >= n |
| Chal(n,s,p) | respond(n+1,s’,s) | Open(n+1) | s->s’ |
| Chal(n,s,p) | altRespond(n+1) | Open(n+1) |
The TLA+ verdict
We ran this new model through TLA+.
The outcome here was better: Alice is always able to progress the channel 🎉. However, there’s a griefing opportunity, where Eve can delay Alice for an amount of time proportional to the current turn number:
- Start in state
Open(0) - Alice calls
forceMove(n, s, Alice) - Eve front-runs with
forceMove(0, s0, Eve), and the adjudicator transitions toChal(0, s0, Eve). - Alice’s force-move fails.
- Eve then calls
respond(1, s0, s1), transitioning the channel toOpen(1). (If she wants to maximise the griefing, she’d wait until the timeout is almost over before calling this, knowing that Alice probably doesn’t have this state anymore). - Alice calls
forceMove(n, s, Alice) - Eve front-runs with
forceMove(1, s1, Eve) - … and so on
It seems that the problem here is at least partially in step 4: the forceMove function
fails because the state of the chain has changed since the time the transaction was
submitted. We realised that there was no reason why a forceMove shouldn’t overwrite an
earlier challenge, and that generally designing operations so that they applied to the
widest possible set of chain states seemed like a good principle.
Attempt 3
For attempt 3, we rewrote forceMove, so that it could also apply in the challenge state.
and no-longer needed to provide the on-chain challenge state. Doing this while retaining
gas efficiency was an interesting challenge, which involved
compressing a bunch of information
into the existing bytes32 channel storage field.
We also did some thinking about the alternative move action, and realised a few things.
Firstly, there was absolutely no reason that altRespond should be limited to increasing
the turn number by 1 - given that a complete supported state is provided, there’s no
reason not to increase the turn counter to that state’s turn number, however much of an
increase that might be. Secondly there was no reason that that should only happen in a
challenge state - being able to increase the turn counter from an open state is a useful
thing to be able to do, for example if you’re going off-line for a long period of time and
want to be able to pre-emptively rule out most challenges beforehand.
Taken together altRespond seemed like a more fundamental operation, so we decided to
rebrand it as checkpoint. We then started to view respond as a more efficient version
of checkpoint, optimized for responding to a force-move with a subsequent state.
We ended up with the following set of operations:
| State | Action | NextState | Requirements |
|---|---|---|---|
| Open(n) | forceMove(m,s,p) | Chal(m,s,p) | m >= n |
| Chal(n,s,p) | forceMove(m,s’,p) | Chal(m,s’,p) | m > n |
| Open(n,s) | checkpoint(m) | Open(m) | m > n |
| Chal(n,s,p) | checkpoint(m) | Open(m) | m > n |
| Chal(n,s,p) | respond(s,s’) | Open(n+1) | s->s’ |
The TLA+ verdict
Success! 🍾 TLA+ found no problems, so by exhaustive search we know that the protocol is sound.
More than this, it’s fairly easy to see that Alice has a strategy where she is able to
advance the channel (or finalize it) with only one transaction: suppose Alice submits
forceMove(n,s,Alice). The only way this transaction can fail is if the on-chain turn
counter has increased to > n, in which case the channel has already advanced, and Alice is
done. If the transaction succeeds, then the adjudicator is in state Chal(n,s,Alice), and
the only possibilities from there is an on-chain increase of the turn counter, or a
timeout and therefore a finalized channel. So by submitting one transaction, Alice
accomplishes her goal.
This is pretty neat, as it allows us to put a strict bound on the number of transactions Alice needs to exit the channel: in the worst case, Alice needs to call k transactions, where k is the number of participants. The first k-1 of these advance the channel until it is Alice’s turn, and as discussed before, the last one is used to force-move herself, after which she doesn’t respond.
Modelling our protocol
In this section we look in more detail about how we set up our TLA+ specification, and exactly what we’re showing above. You can quite safely skip this section, if you’re not interested in the nitty-gritty.
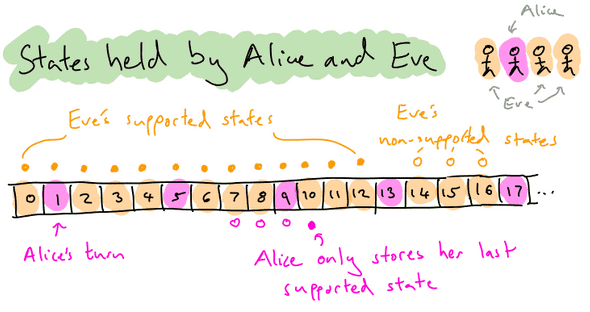
Before we start digging into our TLA+ modelling decisions, it’s worth taking a moment to revisit a key feature of our state channel protocol: the force-move protocol is built around turn taking. Every state exchanged in a channel has a turn number, which can be used to determine which participant has the right to advance the channel at that point. For example, in a two participant channel, the first participant would be responsible for all the even turn numbers, and the second participant for all the odd turn numbers. A state must be signed by the turn taker in order to be part of a valid state transition.
It’s also useful to introduce the concept of a supported state. A supported state, s*,
in a channel with k participants, is a sequence of k states with valid transitions
between them, whose final state is s: s1 -> ... -> sk = s (this is a slight
simplification from the code, but will do for our current purposes). Due to the turn
taking property, a supported state will always contain a signature from each participant.
A supported state is the turn-taking analogue of a fully signed state, signalling that all
participants have participated in advancing the channel to that state.
Our next step is to examine what we’re trying to show, and see if we can reduce the problem to simplify the model that we will feed into TLA+.
We want to show that Alice has a strategy for producing a finalized recent outcome on-chain, within a finite time, regardless of the actions that any of the other participants take. What we will actually show is that the following claim holds:
Channel Progression Claim: if the latest supported state that Alice has seen has turn number n, then she can either (a) obtain a supported state with turn number > n, or (b) ensure the channel finalizes in a state with turn number >= n.
Why is this enough? Suppose Alice’s next turn occurs at turn number n + m. If Alice refuses to sign any state with this turn number, then there can be no supported state at this turn number or higher. Therefore, by applying the channel progression claim m times, the only possible outcome is for the channel to have finalized it a state >= n.
We also need to specify the conditions under which the claim holds. Our model captures the following scenario:
- Alice is an honest participant of the state channel, who holds a supported state with turn number n.
- Alice’s goal is to either (a) obtain a supported state with turn number greater than n, or (b) close the channel in a state with turn number greater than or equal to n
- Alice only stores the last round of states, and therefore only has access to the latest supported state. (This is important as it means that the storage requirements for an honest participant scale with the number of in-channel participants, instead of the total number of signed states.)
- Alice can always get a transaction mined within a challenge period, but does not have the ability to front-run, or prevent transactions from being front-runned.
- Alice only signs a state if (a) it is her turn, and (b) it represents a valid transition from a supported state that she holds.
- Eve is an adversary who controls all other participants in the channel.
- Eve stores the complete history of states exchanged in the channel.
- Eve is willing to sign any state in the past or future, even if it doesn’t represent a valid transition from a state she holds. The only states which she can’t produce a signature for are those on Alice’s turn with turn number > n, as only Alice can sign these, and she hasn’t done so yet.
- Eve has the ability to front-run Alice as many times as she wants, but cannot prevent Alice’s transaction from being mined within the challenge period.
How do we model this scenario with TLA+? If you’re feeling brave, you can jump straight into the code to find out. Otherwise, we’ll continue with a high-level overview here.
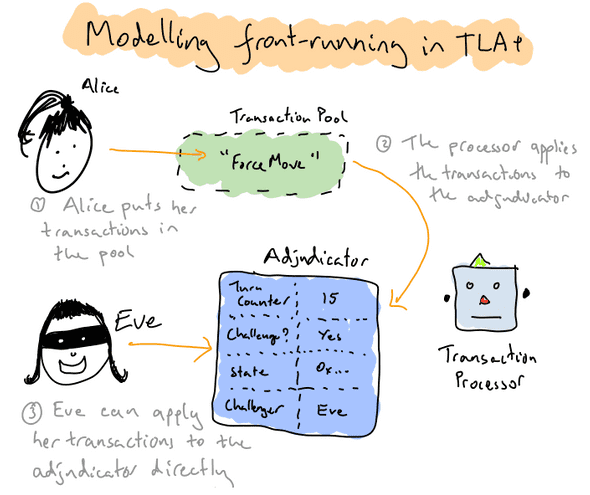
The first thing to understand is that TLA+ specs involve multiple processes that create actions that modify a shared state. When it simulates a system, TLA+ searches all the possible sequences created from interleaving the processes’ actions, stopping each sequence when some condition on the shared state is reached.
In our case, Alice and Eve will be separate processes, and the adjudicator will form part of the shared state. In order to capture the front-running behaviour, we’ll introduce an extra process and piece of state, the transaction processor and the transaction pool. While the Eve process will modify the adjudicator state directly, Alice will be limited to placing a transaction in the transaction pool, which will later be applied to the adjudicator by the transaction processor.
TLA+ has a concept of a ‘fair process’, which is one whose actions won’t be infinitely blocked. This is exactly what we need to model the behaviour that “Eve can front-run Alice as many times as she wants, but Alice will get a transaction in eventually”. We don’t explicitly model the timeout itself, as we know that either Alice or Eve will prevent it if they hold states that allow them to do so. The cases where a timeout would occur are therefore precisely the cases where no further actions are possible, which TLA+ will automatically prevent.
In terms of the success criteria, it pays to strengthen the statement from “Alice can succeed in finite time” to “Alice can succeed within N steps”, where N is a number that we choose. By modifying the statement in this way, we can ensure that TLA+ is searching over a finite, manageable state space.
We also pick a couple of participant numbers to run our simulations with. So specifically we prove statements of the form “in all channels with 2 participants, Alice can obtain her goal within 5 steps”. Of course, this isn’t enough to prove the statements for all channels, but we do get firm guarantees for the channels with a small number of participants, which is all we care about for practical use cases. We also get increased confidence that it will work for arbitrary numbers of participants, and it might be possible to produce an argument that extra participants don’t change things - it certainly feels that way from the model setup.
Summary
In this post we’ve explained how we used TLA+ to prove that the force-move protocol provides the state channel guarantees around being able to withdraw your funds.
Next week we will be moving from theory to practice, with the release of our Web3Torrent project. Web3Torrent enhances the peer-to-peer filesharing of webtorrent, with peer-to-peer micropayments built on top of state channels. We hope it will serve as a demonstration of what is possible with state channels today, and inspire more people to use micropayments/state channels as part of their mechanism design.
Stay tuned!
Written by Tom Close, Magmo team lead @ Consensys R&D. Based off work done by Andrew Stewart. Thanks to Mike Kerzhner and George Knee for comments and suggestions.