Putting the 'state' in state channels

Last week we looked at how to finalize an outcome in a state channel system - how to play the state channel exit game. The system we introduced was a simplified ‘toy’ system, with the state advancing only via complete consensus, and no state transition rules. This week we show how to define and use custom state transition functions, allowing the creation of state channel applications.

Why isn’t complete consensus enough?

Before moving onto these more complex state transitions, it’s worth taking a look at why we need to do this at all. Isn’t complete consensus enough?

First let’s clarify what we mean by complete consensus. By complete consensus we’re talking about a system like that introduced last week, where any change to the outcome of the channel can only occur if all participants explicitly sign the update. This means that at each point of the state channel interaction, every single participant must agree if any progress is to be made.

Imagine, for example, that Alice and Bob are playing a game of chess for a prize. Presumably when they decided to play the game, they both believed that they had a chance of winning. A short while later, Alice plays a winning move, and it becomes completely clear to Bob that he isn’t going to win. What happens now? Under a complete consensus system, Alice’s winning move is only valid if Bob decides to sign it — that’s the only way it will be accepted by the chain. Bob could quite easily refuse to sign, and Alice would have no recourse. Could we add some in-game incentives to punish Bob in this situation? Unfortunately not. To the toy adjudicator, this situation is indistinguishable from the situation where Alice stopped playing, so any incentive we build in to punish Bob here could be used against him by Alice, if she were to choose not to play.

There are many situations where a group of parties agree in advance to a set of rules to govern an interaction, and this is clearly different to agreeing every step of the way. In order to write interesting state channel applications, we need to be able to capture this pattern in our state channel system.

States and transitions

What does it even mean to run an app in a state channel? In a state channel, the calculation is shared between many participants, and progresses as signed states are exchanged between them. The state of the channel, and therefore the state of the calculation, is not a universal property; different participants will have different views of the current state, depending on the states they have signed and the states they hold.

It’s worth saying that this is a pretty different model of execution to most environments, including the blockchain itself. In the blockchain, there is a source of truth, given by the state of the longest chain. This truth might change (in the case of a chain re-org), and might not be known by all participants (in the case of a network partition), but an observer with complete knowledge of the system would be able to determine the current state. In a state channel, this is not the case; an observer with complete knowledge would be able to determine the current state for each participant, but these states could be different.

How do we handle this complexity when building state channel applications? It turns out that there’s a neat way to use state machines to model the execution of a state channel application.

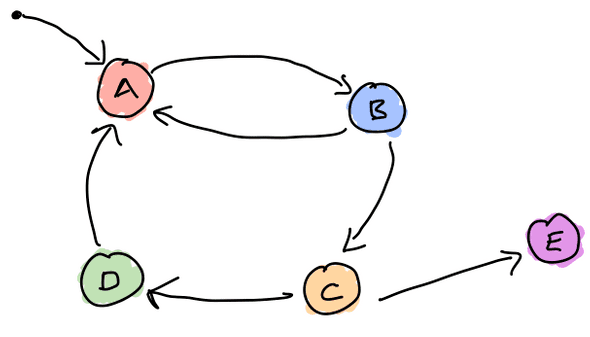
The first step is to construct a the set of allowed states for our state channel, and which transitions are allowed between them. We represent these states as a directed graph, for example:

In the shown machine above we have 5 app states: A, B, C, D, and E. The arrows indicate the allowed transitions: A -> B, B -> A, B -> C, C -> D, C -> E, and D -> A. A is the start state, and E is an end state, as there are no valid transitions leading out of it.

How do we use this diagram to model the execution of a state channel application?

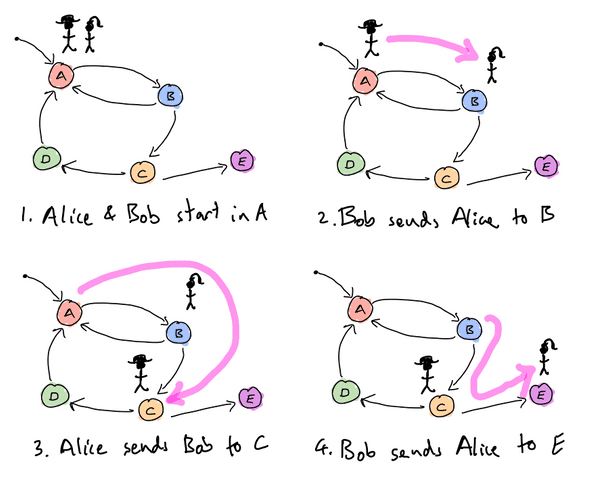
Firstly, we introduce an important rule of our system: that participants should take turns to advance the state. For example, in a two participant channel, this means that the first participant will sign all the even numbered states, and the second participant will sign all the odd numbered states. While there are many possibilities here, intrducing the turn taking rule helps when it comes to analysing which outcomes are finalizable in our system. In our production system, we relax turn taking to a degree, allowing for an optimization where participants can add their signature to one of their opponent’s states.

In terms of the diagram, when a participant signs a state we can think of them ‘moving’ their opponent to the corresponding node on the graph. The rationale here is that by signing a state, they’ve given their opponent the ability to finalize that state; we think of the opponent ‘owning’ the state, and represent that by placing them on top of it. It’s then the opponent’s turn to sign one of the valid transitions out of that state, thereby moving the participant to that state. In a two-participant channel, the participants therefore move around the graph by leap-frogging one another, each taking turns to decide where their opponent should land:

This captures the relative nature of channel execution very naturally; from the diagrams above, it’s clear that Alice and Bob are at different places in the execution of the application. At a given point in time, the participant who’s turn it is has the power: the power to finalize that outcome on-chain, or to send their opponent to one of the following states. By taking their turn, they give up that power and hand it back to their opponent.

Defining rules

In the previous section, we introduced state machines as a tool for modelling state channel applications. But what does this mean in practice? In this section we’ll show the changes that we need to make to our toy system, to enable state channel applications.

For state channel applications to run, we must have a way of defining them, and making their rules available to the state channel. In our system, the application will be defined by a smart contract, that will be deployed on blockchain before the channel is opened. The application definition can be accessed by many channels simultaneously, so the cost of deployment is considered to be a one-off cost, and not included in the running of the channel — just as contract deployment is in a regular dapp.

The contract must adhere to a simple interface, defining a single validTransition function:

interface ForceMoveApp {
    function validTransition(
        State calldata a,
        State calldata b,
    ) external pure returns (bool);
}

The validTransition function accepts two states, and returns true if the transition is valid between them. For the time being, both here and in the state channel system we have created, we restrict the validTransition function to be pure, meaning it can only depend on the data passed in, and cannot read additional state from the blockchain. We believe that it should be possible to remove this restriction in future, but have chosen to keep things simple for the time being.

As well as defining the valid transitions, the function above implicitly defines the valid states and their format: in order to assess whether a transition is valid, the function will first need to decode the data passed in; incorrectly formatted states or states with invalid data will lead to failure. The set of valid states is therefore defined to be the set of states which form part of some valid transition, according to the validTransition function.

We must also extend the definition of the state from our toy system to include the appDefinition and the appData:

struct State {
  address[] participants;
  uint256 channelNonce;
  uint256 turnNum;
  Outcome outcome;
  address appDefinition;  // contract that defines state machine
  bytes appData;         // holds app-specific data
}

As discussed above, the appDefinition stores the address of the contract that defines the validTransition function, that in turn defines the states and transitions for the state channel application running in the channel. Like the participants and channelNonce, the appDefinition must stay constant over the duration of the channel. The appData contains any data the app needs to define the current state. This could be as simple as a string holding the state name, or as complex as the state of a chess board.

So we now have a way of defining a set of application rules, and a place to store them in the state. That’s good, but it doesn’t count for anything unless the outcome finalization game takes these transition rules into account. How do we modify the adjudicator from our toy system to allow for this?

(In the rest of this section we’ll reduce the scope to focus only on two-participant channels. This is just for the ease of explanation — everything here readily generalizes to the n-participant case.)

In our toy model from the last post, a participant could launch a challenge by providing a double-signed state:

// old system, with double-signed states
function launchChallenge(
  State s,
  Signature sig1,
  Signature sig2
)

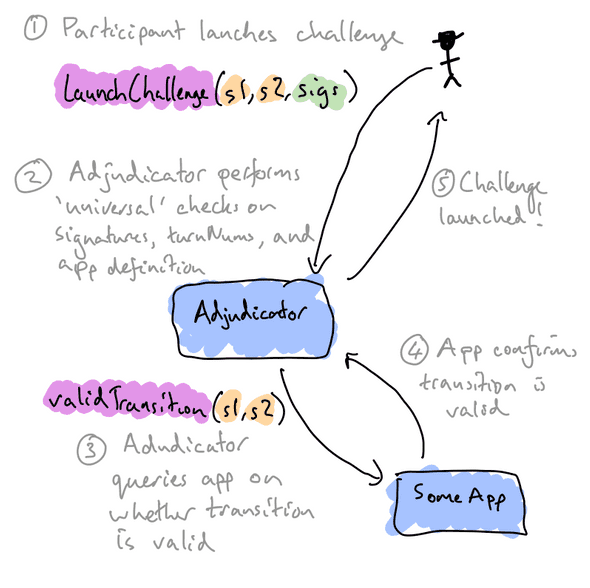
This is no-longer going to work, as states aren’t double-signed in our new system — each participant only signs states when it’s their turn. Instead, to launch a challenge the participant must provide a pair of signed states that represent a valid transition:

// new system, with transition function
function launchChallenge(
  State s1
  State s2,
  Signature sig1,
  Signature sig2
)

This function will take the following actions:

1. Check that sig1 is a valid signature on s1, by the player whose turn it should have been
2. Check that sig2 is a valid signature on s2, by the player whose turn it should have
3. Check that the turnNum has incremented: s2.turnNum == s1.turnNum + 1
4. Check that the appDefinition hasn’t changed: s2.appDefinition == s1.appDefinition
5. Check that the transition is valid according to the appDefinition: ForceMoveApp(appDefinition).validTransition(s1, s2)
6. Move the channel into Challenge state on-chain.

The CounterChallenge also needs to be updated similarly:

// new system, with transition function
function counterChallenge(
  State s1,
  State s2,
  Signature sig1,
  Signature sig2
)

We now have some interesting new behaviour: suppose Bob stops responding, so Alice launches a challenge on turn n. If Bob comes back online, he could counter-challenge with turn n+1, which didn’t previously exist. Then Alice can counter-challenge with turn n+2, and so on. We’ve created a mechanism by which the channel application can progress on-chain, with the chain validating each transition. In this scenario, you can think of the challenge as a way of forcing your opponent to take a move, with the threat that the channel closes with the current outcome if they don’t.

In this situation, where one participant is temporarily unavailable but then returns, there’s no reason to force the entire interaction to play out on-chain from that point onwards. The production state channel system that we’ve created has the property that it’s possible to recover from an on-chain challenge, and complete the state channel interaction off-chain.

What’s next?

In this post we looked at how to add extra data and transition rules to state channels, allowing us to build applications that can run in state channels. We explained how to add machinery so that participants can unilaterally advance the state a small amount, according to these pre-agreed rules — a crucial feature for enabling the full range of applications. In the next couple of posts, we’ll look at a working example of a state channel application, and present the state channel system we’ve been working on, which contains all the features we’ve covered so far along with optimizations and a full set of safety features.

Until next time!

Written by Tom Close, Magmo team lead @ Consensys R&D